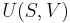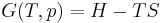Thermodynamic equilibrium

In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance. In a state of thermodynamic equilibrium, there are no net flows of matter or of energy, no phase changes, and no unbalanced potentials (or driving forces), within the system. A system that is in thermodynamic equilibrium experiences no changes when it is isolated from its surroundings.

In non-equilibrium systems there are net flows of matter or energy, or phase changes are occurring; if such changes can be triggered to occur in a system in which they are not already occurring, it is said to be in a metastable equilibrium.

Thermodynamics
Branches Classical · Statistical · Chemical Equilibrium / Non-equilibrium Thermofluids
Laws Zeroth · First · Second · Third
Systems State: Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency
System properties Property diagrams Intensive and extensive properties State functions: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat
Material properties Specific heat capacity  Compressibility  Thermal expansion  Property database
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Table of thermodynamic equations
Potentials Free energy · Free entropy Internal energy Enthalpy Helmholtz free energy Gibbs free energy
History and culture Philosophy: Entropy and time · Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics History: General · Heat · Entropy · Gas laws Perpetual motion Theories: Caloric theory · Vis viva Theory of heat Mechanical equivalent of heat Motive power Publications: "An Experimental Enquiry Concerning ... Heat" "On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines of: Thermodynamics · Heat engines Art: Maxwell's thermodynamic surface Education: Entropy as energy dispersal
Scientists Daniel Bernoulli Sadi Carnot Benoît Paul Émile Clapeyron Rudolf Clausius Hermann von Helmholtz Constantin Carathéodory Pierre Duhem Josiah Willard Gibbs James Prescott Joule James Clerk Maxwell Julius Robert von Mayer William Rankine John Smeaton Georg Ernst Stahl Benjamin Thompson William Thomson, 1st Baron Kelvin John James Waterston

Contents 1 Overview 1.1 Conditions for equilibrium 2 Local and global equilibrium 3 Types of equilibrium 3.1 Thermal equilibrium 3.2 Quasistatic equilibrium 3.3 Non-equilibrium 4 General references 5 Footnotes 6 External links

Overview

Classical thermodynamics deals with dynamic equilibrium states. The local state of a system at thermodynamic equilibrium is determined by the values of its intensive parameters, such as pressure or temperature. To be specific, thermodynamic equilibrium is characterized by the minimum of a thermodynamic potential, such as the Helmholtz free energy, i.e., systems at constant temperature and volume:

A = U – TS;

Or as the Gibbs free energy, i.e., systems at constant pressure and temperature:

G = H – TS.

where T = temperature, S = entropy, U = internal energy and H = enthalpy. The Helmholtz free energy is often denoted by the symbol F, but the use of A is preferred by IUPAC [2].

The process that leads to a thermodynamic equilibrium is called thermalization. An example of this is a system of interacting particles that is left undisturbed by outside influences. By interacting, they will share energy/momentum among themselves and reach a state where the global statistics are unchanging in time.

Conditions for equilibrium

By considering the differential form of thermodynamic potentials, the following relationships can be derived:

• For a completely isolated system, ΔS = 0 at equilibrium.
• For a system at constant temperature and volume, ΔA = 0 at equilibrium.
• For a system at constant temperature and pressure, ΔG = 0 at equilibrium.

The various types of equilibriums are achieved as follows:

• Two systems are in thermal equilibrium when their temperatures are the same.
• Two systems are in mechanical equilibrium when their pressures are the same.
• Two systems are in diffusive equilibrium when their chemical potentials are the same.
• All forces are balanced.

Local and global equilibrium

It is useful to distinguish between global and local thermodynamic equilibrium. In thermodynamics, exchanges within a system and between the system and the outside are controlled by intensive parameters. As an example, temperature controls heat exchanges. Global thermodynamic equilibrium (GTE) means that those intensive parameters are homogeneous throughout the whole system, while local thermodynamic equilibrium (LTE) means that those intensive parameters are varying in space and time, but are varying so slowly that, for any point, one can assume thermodynamic equilibrium in some neighborhood about that point.

If the description of the system requires variations in the intensive parameters that are too large, the very assumptions upon which the definitions of these intensive parameters are based will break down, and the system will be in neither global nor local equilibrium. For example, it takes a certain number of collisions for a particle to equilibrate to its surroundings. If the average distance it has moved during these collisions removes it from the neighborhood it is equilibrating to, it will never equilibrate, and there will be no LTE. Temperature is, by definition, proportional to the average internal energy of an equilibrated neighborhood. Since there is no equilibrated neighborhood, the concept of temperature breaks down, and the temperature becomes undefined.

It is important to note that this local equilibrium may apply only to a certain subset of particles in the system. For example, LTE is usually applied only to massive particles. In a radiating gas, the photons being emitted and absorbed by the gas need not be in thermodynamic equilibrium with each other or with the massive particles of the gas in order for LTE to exist. In some cases, it is not considered necessary for free electrons to be in equilibrium with the much more massive atoms or molecules for LTE to exist.

As an example, LTE will exist in a glass of water that contains a melting ice cube. The temperature inside the glass can be defined at any point, but it is colder near the ice cube than far away from it. If energies of the molecules located near a given point are observed, they will be distributed according to the Maxwell-Boltzmann distribution for a certain temperature. If the energies of the molecules located near another point are observed, they will be distributed according to the Maxwell-Boltzmann distribution for another temperature.

Local thermodynamic equilibrium does not require either local or global stationarity. In other words, each small locality need not have a constant temperature. However, it does require that each small locality change slowly enough to practically sustain its local Maxwell-Boltzmann distribution of molecular velocities. A global non-equilibrium state can be stably stationary only if it is maintained by exchanges between the system and the outside. For example, a globally stably stationary state could be maintained inside the glass of water by continuously adding finely powdered ice into it in order to compensate for the melting, and continuously draining off the meltwater. Transport phenomena are processes that lead a system from local to global thermodynamic equilibrium. Going back to our example, the diffusion of heat will lead our glass of water toward global thermodynamic equilibrium, a state in which the temperature of the glass is completely homogeneous.^[1]

Types of equilibrium

Thermal equilibrium

Thermal equilibrium is achieved when two systems in thermal contact with each other cease to have a net exchange of energy. It follows that if two systems are in thermal equilibrium, then their temperatures are the same.^[2]

Thermal equilibrium occurs when a system's macroscopic thermal observables have ceased to change with time. For example, an ideal gas whose distribution function has stabilised to a specific Maxwell-Boltzmann distribution would be in thermal equilibrium. This outcome allows a single temperature and pressure to be attributed to the whole system. Thermal equilibrium of a system does not imply absolute uniformity within a system; for example, a river system can be in thermal equilibrium when the macroscopic temperature distribution is stable and not changing in time, even though the spatial temperature distribution reflects thermal pollution inputs.

Quasistatic equilibrium

Quasistatic equilibrium is the quasi-balanced state of a thermodynamic system near to thermodynamic equilibrium, in some sense. In a quasistatic or equilibrium process, a sufficiently slow transition of a thermodynamic system from one equilibrium state to another occurs such that at every moment in time the state of the system is close to an equilibrium state. During a quasistatic process, the system reaches equilibrium much faster, almost instantaneously, than its physical parameters vary.

Non-equilibrium

Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Most systems found in nature are not in thermodynamic equilibrium because they are changing or can be triggered to change over time, and are continuously and discontinuously subject to flux of matter and energy to and from other systems. The thermodynamic study of non-equilibrium systems requires more general concepts than are dealt with by equilibrium thermodynamics. Many natural systems still today remain beyond the scope of currently known macroscopic thermodynamic methods.

General references

• Cesare Barbieri (2007) Fundamentals of Astronomy. First Edition (QB43.3.B37 2006) CRC Press ISBN 0-7503-0886-9, 9780750308861
• Hans R. Griem (2005) Principles of Plasma Spectroscopy (Cambridge Monographs on Plasma Physics), Cambridge University Press, New York ISBN 0-521-61941-6
• C. Michael Hogan, Leda C. Patmore and Harry Seidman (1973) Statistical Prediction of Dynamic Thermal Equilibrium Temperatures using Standard Meteorological Data Bases, Second Edition (EPA-660/2-73-003 2006) United States Environmental Protection Agency Office of Research and Development, Washington DC [1]
• F. Mandl (1988) Statistical Physics, Second Edition, John Wiley & Sons

Footnotes

External links

• Breakdown of Local Thermodynamic Equilibrium George W. Collins, The Fundamentals of Stellar Astrophysics, Chapter 15
• Thermodynamic Equilibrium, Local and otherwise lecture by Michael Richmond
• Non-Local Thermodynamic Equilibrium in Cloudy Planetary Atmospheres Paper by R. E. Samueison quantifying the effects due to non-LTE in a atmosphere
• Local Thermodynamic Equilibrium
• Xchanger Inc, webpage Calculator for thermodynamic equilibrium of pneumatic conveying air and conveyed product.